The Checker Maven
The World's Most Widely Read Checkers and Draughts Publication
Bob Newell, Editor-in-Chief
Published every Saturday morning in Honolulu, Hawai`i
Noticing missing images? An explanation is here.
CV-1 Solution
BLACK
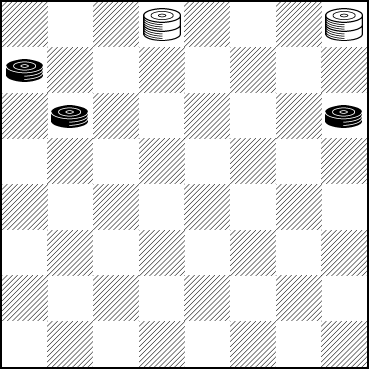
WHITE
White to Play and Draw
W:WK2,K4:B5,9,12
Brian Hinkle's 2x3 problem published two weeks ago, which we've called CV-1, is a deep and difficult setting. ACF Bulletin editor Jim Loy wrote to Brian saying that there are probably a thousand drawing possibilities and it would take a year to unravel. This is surely one of the best 2x3 problems ever published. There is no doubt that the draw is subtle, finely balanced, and relies on moves which at times don't seem intuitive or natural.
It's impossible for us to go into everything in a single column, so we'll just show a couple of options and let you use your computer to work through the many different variations.
When you're done, Brian would like to know what your favorite drawing line might be. Write to him at sbhinkle@charter.net with your comments.
Brian points out three major drawing themes: a line that ends in Payne’s Double Corner Draw, one that ends in Roger’s Draw, and one that ends in Dr. Brown’s Draw (as in Boland's Famous Positions page 19).
Brian elaborates: If Black keeps the man on 12, then Roger’s Draw is needed. If Black advances the man on 12 to 20, then Payne’s Double Corner Draw is in order. Finally, the important transposition into Dr. Brown’s Draw shows why White must start with 4-8* and 8-11*.
Wow!
First, we'll show Brian's chosen solution, the one he thinks best represents the trunk line. The solution is very long, and you may wish to use this animation. Notes were provided by Brian.
| 1. | ... | 4-8 |
Note that the seemingly "obvious" 2-6 (chasing with the king) will lose, as will 2-7.
| 2. | 12-16 | 8-11 |
| 3. | 16-19 | 11-15 |
| 4. | 19-23 | ... |
Or 19-24 15-10* 24-27 2-6 (chasing with the king is now correct) 9-13 10-14 27-31 6-10 31-27 10-15 27-23; this is the same draw as in Dr. Brown's Famous Positions, p.19, colors reversed.
| 4. | ... | 15-18 |
| 5. | 23-26 | 18-22 |
| 6. | 26-31 | 2-6 |
| 7. | 9-13 | 6-10 |
| 8. | 31-27 | 10-14 |
| 9. | 27-23 | 14-10 |
| 10. | 23-19 | 10-14 |
| 11. | 19-15 | 22-25 |
| 12. | 15-11 | 25-22 |
| 13. | 11-7 | 22-25 |
| 14. | 7-2 | 25-22 |
Stopping the Black king with 14-10? might be tempting but it loses by 15. 13-17 10-14 16. 17-21 25-22 17. 2-6 14-18 18. 6-9 18-23 19. 9-13 23-26 20. 5-9 26-23 21. 9-14 23-26 22. 14-17 22-18 23. 17-22 Black Wins.
| 15. | 2-6 | 14-18 |
| 16. | 6-9 | 18-23 |
| 17. | 9-14 | 23-26 |
| 18. | 14-17 | 22-18 |
| 19. | 17-21 | 18-22 |
| 20. | 21-17 | 22-18 |
| 21. | 5-9 | 26-23 |
| 22. | 17-14 | 18-22 |
| 23. | 14-10 | 23-18 |
White has to defend accurately; if 23-26? then 24. 10-15 26-23 25. 9-14 23-26 26. 14-18 22-25 27. 13-17 Black Wins.
| 24. | 10-7 | 22-25 |
| 25. | 7-11 | 25-22 |
| 26. | 11-16 | 22-25 |
| 27. | 16-20 | 25-22 |
| 28. | 20-24 | 22-25 |
| 29. | 24-27 | 25-22 |
| 30. | 27-31 | 22-25 |
| 31. | 31-26 | 25-30 |
| 32. | 26-31 | 30-25 |
| 33. | 31-27 | 25-22 |
| 34. | 27-24 | 22-25 |
| 35. | 24-19 | 25-22 |
| 36. | 19-16 | 22-25 |
| 37. | 16-11 | 25-22 |
| 38. | 11-7 | 22-25 |
| 39. | 7-2 | 25-22 |
| 40. | 2-6 | 22-25 |
| 41. | 6-1 | 25-22 |
| 42. | 1-5 | 18-23 |
| 43. | 9-14 | 23-26 |
| 44. | 5-1 | 26-23 |
Precision play is required: if 26-30? then 45. 1-6 30-26 46. 6-10 26-23 47. 10-15 23-26 48. 14-18 22-25 49. 13-17 Black Wins.
| 45. | 1-6 | 22-18 |
| 46. | 6-9 | 18-22 |
| 47. | 14-17 | 22-18 |
| 48. | 9-6 | 23-26 |
| 49. | 6-2 | 26-30 |
With the Black king way back on square 2, White must now force the Black piece on 17 into square 21. If 18-22? then 50. 2-7 22-18 51. 7-11 26-30 52. 17-21 18-22 53. 11-15 30-26 54. 15-19 26-30 55. 19-23 22-26 56. 23-18 26-31 57. 13-17 31-26 58. 18-14 26-31 59. 17-22 Black Wins.
| 50. | 2-7 | 30-25 |
| 51. | 17-21 | 25-22 |
| 52. | 7-11 | 18-23 |
| 53. | 11-16 | 23-27 |
| 54. | 16-19 | 27-32 |
| 55. | 19-23 | 32-28 |
| 56. | 23-27 | 28-32 |
| 57. | 27-31 | 32-28 |
| 58. | 31-27 | 28-32 |
| 59. | 27-24 | 32-28 |
| 60. | 24-19 | 28-32 |
| 61. | 19-15 | 32-27 |
| 62. | 15-10 | 27-23 |
| 63. | 10-14 | 23-26 |
| 64. | 14-10 | 26-23 |
Drawn. An example of "one holds two."
Next, we'll show a line that we took from the KingsRow engine, using its 10-piece endgame database. Brian called this one, "The King Goes on a Vacation." An animation can be found here.
| 1 | ... | 4-8 |
| 2. | 9-14 | 8-11 |
| 3. | 5-9 | 2-7 |
| 4. | 14-18 | 7-10 |
| 5. | 18-22 | 11-15 |
| 6. | 22-25 | 15-18 |
| 7. | 25-30 | 18-23 |
| 8. | 9-13 | 10-14 |
| 9. | 12-16 | 14-10 |
Brian comments, "This white king decides that now is a good time to 'go on vacation' because the other king on 23 is doing all of the heavy defensive lifting."
| 10. | 13-17 | 10-7 |
| 11. | 17-22 | 7-3 |
| 12. | 16-20 | 23-27 |
| 13. | 22-25 | 3-7 |
The computer here gave 22-26 which no human would likely play.
| 14. | 25-29 | 7-10 |
| 15. | 29-25 | 10-15 |
| 16. | 25-22 | 27-32 |
This has now transposed into the solution of Brian Hinkle's A Walk Through Time from Ed Salot's problem composing contest 39.
| 17. | 22-26 | ... |
20-24 is interesting, hoping for the blunder 32-28? Black Wins. But if White avoids the trap, 20-24 only draws.
| 17. | ... | 32-27 |
| 18. | 26-22 | 27-32 |
| 19. | 22-17 | ... |
The computer gives 22-26, leading to repetition, but this is another try.
| 19. | ... | 15-11! |
Not 15-18, which loses.
| 20. | 17-14 | ... |
The computer gives 17-22.
| 20. | ... | 11-15 |
| 21. | 30-26 | 32-27 |
| 22. | 14-9 | 15-10 |
| 23. | 26-22 | 10-15 |
| 24. | 9-14 | 15-19 |
| 25. | 14-18 | 19-24 |
| 26. | 18-15 | 24-28 |
| 27. | 15-19 | 28-32 |
| 28. | 22-18 | 32-28 |
| 29. | 19-23 | 28-32 |
| 30. | 23-19 | 32-28 |
Etc. Drawn. A double corner defense which will work as long as the remaining single Black man can't crown.
There is much, much more to this problem and indeed one could spend a year on it. We'll just copy the line seen in many an advanced math textbook: "The rest is left as an exercise for the reader."
Our thanks to Brian Hinkle for this problem, and to Brian and Jim Loy for much of the analysis.![]()
All Is Not Lost

Some situations seem pretty hopeless. In the image above, things don't look so great for our hero. But you might guess that he's not one to easily give up.
The same is often true on the checkerboard. Take a look at the position below.

WHITE
White to Play and Win
W:WK8,10,14,15,30,32:B1,2,3,12,K18,23
White is going to lose a piece and nothing will stop that. But indeed all is not lost---there still is a way to win, if you don't give up hope and can find your way through. This isn't quite a speed problem, but it isn't all that difficult, either. Stay the course and win the battle, then click on Read More to verify your victory.
And stay safe and well, checker fans, wherever you are.![]()
Checker Maven Special Edition

Many of us in the checker community are older and may have underlying health issues that put us at higher risk from the current virus epidemic, so we need to stay at home. Many others are under mandate to do the same. But no matter who we are or where we are, it's a good idea.
That gives us a lot of potentially unoccupied time. Correspondent Brian Hinkle suggested that this would be a good moment for checker fans to attempt deep and difficult checker problems.
Hence this special edition, in which we present one of Brian's own compositions, one which he considers to be challenging indeed. We won't be publishing the solution for two weeks in order to give you a chance to really dig into it.
Even if you're closer to novice than expert, this problem is worth your while. Maybe you'll solve it, maybe you won't, but you'll likely pass quite some time with good checker entertainment, and perhaps be distracted a little when you need it the most.
Here's the position, without further commentary. Good luck!
BLACK

WHITE
White to Play and Draw
W:WK2,K4:B5,9,12
Be safe and well, checker fans, wherever you are.![]()
Fatal Squeeze

This woman is either brave and skilled, or courting disaster, risking a fatal squeeze from a huge, powerful snake.
Today in our Checker School series, we return to the adventures of Skittle and Nemo, as found in Andrew Banks' Checker Board Strategy. The title of our column is a big hint for the solution to the problem below, so we're not giving much more away when we note that Skittle warned Nemo, "Always look well before you squeeze a piece."
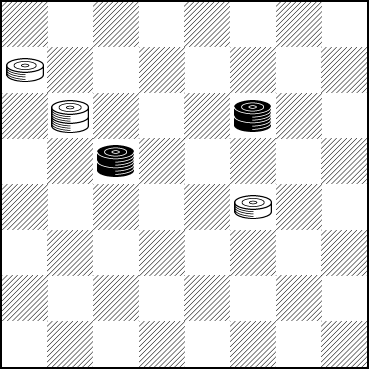
BLACK
Black to Play and Win
B:W14,K24,28:BK19,K22
White has just blundered badly by playing 27-24. (White really should have won, so for extra credit, give a better move for White.)
This one is super easy and probably will be solved at once by players of any level above novice. (We like to have a balance in our columns; we don't want to squeeze anyone out by just publishing difficult positions.) When you've found the solution, check your work by squeezing the mouse button with the cursor on Read More.![]()
Some Things Don't Work Out

Looks like something didn't work out in the photo above. Maybe whoever is responsible needs to try again, or try a little harder in the first place.
This month's speed problem--- we'll call it that because it's on the easy side, if not quite in the 10 second category--- illustrates the concept. Not everything works out. If you can see what doesn't work out, you'll find the solution right away.

WHITE
White to Play and Draw
W:W14,15,19,23,31:B6,7,8,12,16
Once again we won't use our Javascript clock; just do the best you can to sort out right from wrong. And something that's right for sure: clicking on Read More will show you the solution.![]()
Leap Year Day

It's a rare occurrence for The Checker Maven: we're publishing a column on February 29, or Leap Year Day. It's something that will happen only once every 28 years.
Leap Year is an interesting and rather brilliant concept. You can read about it online, so we'll only say that it's the way our calendar, the Gregorian calendar, keeps in amazingly close synchronization with the solar calendar (we'll perhaps discuss the concept of 'leap seconds', which deal with the gradual slowing of the earth's rotation, at another time).
What has this got to do with our game of checkers? Well, we think Leap Year Day is a great occasion for a checker problem with a lot of leaping--- namely, a stroke problem! So, without further ado, here's today's position.

WHITE
White to Play and Win
W:W12,K14,15,K17,19,23,24,27,K32:B1,4,5,7,18,20,K21,26,K29
We'd have to rate this one as quite high on the difficulty scale, especially if you try to sight solve without moving the pieces. But the solution is very pleasing--- if you can find it. And yes, there's lots and lots of leaping.
So take a leap of faith (in your powers of analysis) and jump right into this problem. Later on, when you've either solved it or become hopping mad with frustration, pounce on Read More to see the solution.![]()
02-22-2020

This column will appear on a very interesting date, in a very interesting week. How often do we see dates like 02-20-2020 and 02-22-2020? There will be another such repetition in 2022, but then we'll have to wait until 03-03-3003 for something similar. Perhaps The Checker Maven may have even ceased publication by then, although one never knows.
This week's dates give a bit of a hint toward today's problem and today's theme. See if you can figure it out. Here's the position.

WHITE
White to Play and Win
W:B10,17,20:W30,31,32
This is definitely not an easy problem. Although it will be made easier if you can correctly identify the theme, it may still be at or near master level. But no matter what your skill level, we urge you to try it. And no matter how much or how little progress you make, please take the time to click on Read More to see the solution and one of the most interesting sets of notes and commentary we've published in recent times.![]()
Symmetrical

Symmetry. We've featured this before, and it's worth featuring again, as it's a powerful concept. In art, symmetry is well-known, but the idea occurs in many realms, even including philosophy. And symmetry can be a very effective tool in the sciences, enabling us to demonstrate something such as the fact that the gravitational force between two isolated objects has to be in a straight line between them.

All of this brings us, in a certain way, to today's Checker School study, shown below.

BLACK
Black to Play and Draw
B:W16,K18,19,23:BK13,K17,22
Today's position exhibits a certain kind of symmetry, at least in overall appearance, although forces are unbalanced. And there's the challenge: how is Black to achieve a piece-down draw? It's all a matter of technique and knowledge, and yes, it can be done, as unlikely as it may appear.
So give this a balanced look and see how you can even things up. When you've found a solution, move your mouse--- symmetrically--- to Read More to check your work.![]()
Barker's Triangle

In our modern day, a certain Jack Barker has written a book about "The Conjoined Triangles of Success" which supposedly will guide you to running a startup company that thrives. Engineering and Manufacturing meet Sales and Growth along the hypotenuse of Compromise.
We can't really speak to this methodology, but there is another Barker and another triangle that predates the modern interpretation by over 100 years. It's a study by the famed checkerist C. F. Barker, and his position, shown below, is often known as Barker's Triangle.

WHITE
White to Play and Draw
W:W11,K15,K22:BK4,5,23,28
We've got to say this problem is one of the most instructive we've ever come across. Why it's called a 'triangle' will become clear when you find the solution. So, give it a good effort and then triangulate your mouse on Read More to see how it's done.![]()
A Winter Saturday at the Beacon Cafe

The holidays were over and now North Dakota was in the depths of winter. With even daytime temperatures often well below zero and plenty of snowy days, residents of Bismarck tended to spend as little time out of doors as possible.
Sal had arrived early at the Beacon Cafe for the regular Saturday afternoon session of the Coffee and Cake Checker Club, and he was warming himself with a steaming hot cup of Deana's coffee. Deana, the proprietor, made good coffee and even better desserts, surely the best for miles around.

Sal
The boys--- that's what Sal called the other members of the club, even though they were all over fifty--- were still stinging a little from the beating they took when Sal challenged them, just before the holidays, with his friend Brian's 6x6. Sal chuckled to himself. They were going to get another surprise today.
The boys started to file in out of the cold, all of them wearing winter parkas, wool caps, heavy gloves, and fur-lined boots. One by one they joined Sal at the big booth in the back. Wayne, Louie, Larry, and Delmer were there, and to everyone's surprise, so was Kevin, who only showed up a couple of times a year.

Spooler
"Hey Spooler, seeing you're here for a change, you buying today?" Wayne asked. Kevin went by the nickname Spooler for reasons not really known to anyone.
"Buying what?" Kevin asked innocently.

"Caramel rolls," Deana called over from behind her counter. "Just baked a fresh tray of them. Great with coffee, especially on a day like this." Deana was, among many other things, a great promoter of her wares.
Everyone looked at Sal. "Okay, what've you got?" Larry asked. "Make it a good one so Spooler can buy for everyone."
"Just so happens," Sal said, "there's one from Ed that he calls 'Code Breaker.'" Ed, from Pennsylvania, was Sal's other checker penpal.
"Is it as hard as that one from Brian last month?" Delmer asked.
"See for yourself," Sal said, as he set up the following position on his favorite checkerboard.

WHITE
White to Play and Win
W:B2,3,12,13,20,22,26,K27:W10,16,24,25,K8,K18,K19
"Oh, that doesn't look too ..." Spooler began, but then he stopped. "Uh ... wait a minute ..."
Everyone laughed. But only for a moment, for they were all soon busy examining the checkerboard.
"Fifteen minutes I'll give you," Sal said, but the concentration was so deep his words went unheard.
"Time's up," Sal said a quarter of an hour later.
"I've got it," Larry said. "Let me show you. It's just like ..."
"NO!" Wayne, Delmer, and Louie shouted all at once. "We want Spooler to pay today," Delmer pointed out.
"Aw, c'mon guys, I don't know how to do it," Spooler said. "You just want me to pay because I don't come every week.
Heads nodded in unison. "Not even every month," Wayne pointed out.
"But, okay," Spooler said. "I'll buy ... if Larry really has it right."
This really fine problem by master problemist Ed Atkinson is challenging but solvable, and the promise of one of Deana's caramel rolls would be too much for anyone to resist. Can you solve it? We urge you to give it a good trial. Now, we don't know if anything like The Beacon Cafe is in your area, but coffee and cake are certainly in order if you make a genuine effort. When you're ready, click on Read More for the solution and the rest of the story.![]()
The Checker Maven is produced at editorial offices in Honolulu, Hawai`i, as a completely non-commercial public service from which no profit is obtained or sought. Original material is Copyright © 2004-2025 Avi Gobbler Publishing. Other material is public domain, as attributed, or licensed under Creative Commons. Information presented on this site is offered as-is, at no cost, and bears no express or implied warranty as to accuracy or usability. You agree that you use such information entirely at your own risk. No liabilities of any kind under any legal theory whatsoever are accepted. The Checker Maven is dedicated to the memory of Mr. Bob Newell, Sr.

