The Checker Maven
The World's Most Widely Read Checkers and Draughts Publication
Bob Newell, Editor-in-Chief
Published every Saturday morning in Honolulu, Hawai`i
Noticing missing images? An explanation is here.
The Depths of Winter

North America is in the depths of winter once again; it's the time of year when there's been enough winter weather that you really, really want spring to come. But you'll have to wait another eight weeks or so for that.
Fortunately, checkers never gets tiresome, and if you've got to be indoors, what better way than with a hot beverage and a fine checker study? The one below, attributed to old-time player Charles Hefter, is surprisingly good.

BLACK
Black to Play and Win
B:W19,18:BK20,K17.
Looks easy, doesn't it? Black has two kings and White has but two ordinary men. But in fact winning this position requires careful play.
Can you get the full score or will you tire of the effort? Of course you won't, and clicking on Read More will allow you to check your solution.![]()
Two For The Price Of One

Two-for-the-price-of-one promotions are certainly popular in the world of marketing, making the buyer believe they're getting a good deal. Sometimes you do get a good price, and at other times (such as in the photo above), not so much. We occasionally refer to some bad deals as giving you "fifty percent off twice the price" or what is known in French as a "fausse solde."
But to start off February we have, indeed, two checker problems for the price of one, and it's definitely a good deal. (Not that you ever have to pay to read The Checker Maven, of course.)
The first situation is a true speed problem, and a rather nice one sent to us by regular contributors Lloyd and Josh Gordon. It's not terribly hard, probably of the 30 second variety.
BLACK
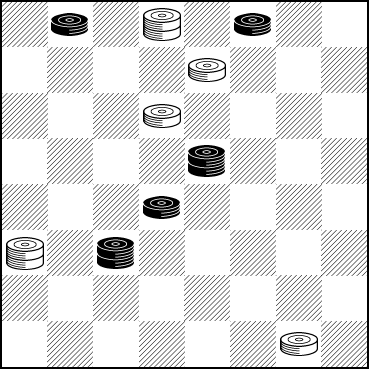
WHITE
White to Play and Draw
W:W32,K21,10,7,K2:BK22,18,K15,3,1.
But what is interesting, though, is that if White plays 2-6 the game is lost, yet that's the move one might make reflexively. This one is somewhat longer and a bit more difficult, and can't really be called a speed problem.
WHITE

BLACK
Black to Play and Win
B:W32,K21,10,7,K6:BK22,18,K15,3,1.
Don't sell out; instead, double down on these two problems, then click on Read More to see the solutions.![]()
The New Year Has Arrived

The New Year has sped in with a bang. The holidays are over and it's back to work and back to school.
We hope your "work" will include your checker game, and to that end we have a speed problem provided by regular contributors Josh and Lloyd Gordon of Toronto. We won't run our Javascript clock this time, as we think you should be allowed at least a minute or two to solve it. We'll even give you a hint: Read the first sentence of this column again.

BLACK
Black to Play and Win
B:WK11,13,17,18,21,28,30:B5,6,9,12,19,K27,K31.
Can you rush to a solution and work out the winning moves? When you've got it, click on Read More to see the solution.![]()
The New Year Is Coming In

We're publishing this column just ahead of New Year's Eve. Now, usually our New Year's column appears just after the holiday, and we like to publish an easier problem in case you, well, indulged in a bit of celebration, such as the Honolulu revelers above are doing.
But you've got until Sunday night this year (2017) which gives you most of a weekend, so we don't at all feel guilty about publishing something a little more difficult.

BLACK
Black to Play and Win
B:W28,27,24,22,19,18,16:B20,13,12,11,7,3,2.
This is indeed fascinating. Black seems hemmed in and has little in the way of safe moves. How can he possibly win it?
Finding the solution actually isn't all that hard, and it's a very pleasing one. Can you do it before the year runs out? That's your challenge, to ring in the New Year with a checker victory. Clicking on Read More will allow you to verify your work.![]()
Holiday Coffee and Cake

It's the holiday season, which means family, friends, and feasting. So, we at The Checker Maven thought, why not treat our readers to more coffee and cake?
Our old friend Brian Hinkle sent us a composition of his own that he thought would make a great "coffee and cake" problem, and we heartily agree. It's a 3x3 twin with, as Brian points out, the unique feature that no matter who plays, White wins.
So, in between courses at your holiday dinner, or maybe after dinner with a second helping of coffee and cake, you might want to try this one out. We think it's easier when Black is to play, but you'll have to decide that for yourself.

BLACK
Black to Play, White Wins
B:W30,26,24:B17,13,12.

WHITE
White to Play and Win
W:W30,26,24:B17,13,12.
Can you earn that coffee and cake? We'll give you credit if you make a good effort, after which you can click on Read More to see the solutions.![]()
How Fast Can You Win It?

"Fast Win" is, it seems, a computer shop on the island of Cebu in the Philippines. We can't explain how the name came about, and frankly it would seem to apply more to checkers or some other game than to computers. We have seen so-called "fast win" computerized slot machines, but we suspect that the fast winner there would be the operating venue.
Now, every once in a while we publish an "oddball" problem. This one is original, although it is inspired by something published long ago. The idea is to find a "fast win."

WHITE
White to Play and Win
W:W32,31,30,29,28,27,26,25,24,23,22,21:BK7.
Well, sure, it's completely obvious that White wins, but what's the fastest way to win, given an effort by Black to hold out as long as possible?
It's not all that difficult, and we'll give you a large hint: we found a 5-move win. Can you go us one better?
Give it a try, and see if you can either make Black hold out longer or White win more quickly. You can see our own solution by clicking on Read More.![]()
Thanksgiving Weekend 2017

Every year we express our delight when our favorite family holiday, Thanksgiving, rolls around on the calendar. What's not to like? It's uniquely American in origin, it appeals to all faiths and creeds, and it's a great time to show our gratitude for the things we have in our lives, and there are more of those than you might think at first glance.
On special occasions we like to turn to Tom Wiswell. Today we present one of his traditional "coffee and cake" problems, developed years ago over that very same pair of treats with Milton Loew. Mr. Loew at the time was just 16 years old and already the U.S. Junior Champion. Here's the position, which came from one of Mr. Loew's tournament games.
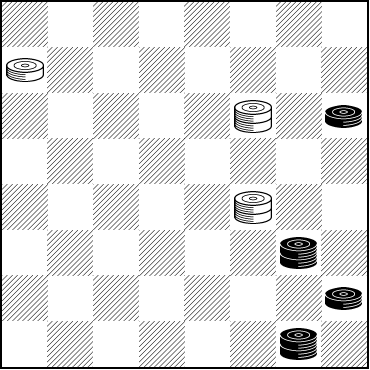
WHITE
White to Play and Draw
W:WK19,K11,5:BK32,28,K24,12.
White is a piece down and is under attack. But Black has some problems, too. Can you win "coffee and cake" from your checker friends with this one? It's not as hard as you may think. Give it a try, and be thankful that you can always click on Read More to see the solution.![]()
Robertson's Tool

If you've ever lived in Canada, you'll know about the Robertson screwdriver, invented by Canadian P. L. Robertson around 1908. Robertson screws and screwdrivers supposedly have many practical advantages, though we won't go into them here.
Would P. L. Robertson be related to D. Robertson of Glasgow? Probably not, but if the Canadian Robertson was known for practicality in tools, Glasgow Robertson might equally be known for practicality in checker settings.
Consider the problem below.
WHITE
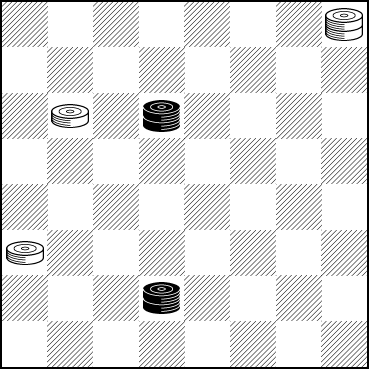
BLACK
Black to Move and Draw
B:WK29,24,12:BK23,K7.
This is, indeed, a practical situation; Black has two Kings but is down a piece. Pulling off a draw in this situation would be rather a success.
Can you do it? Keep your grip on your best checker tools, and give this one a turn or two. You can see the solution by applying your mouse to Read More.![]()
Spectacular Finale

A spectacular finale: It's the goal of many a concert, show, or special event, and it sends everyone home just as pleased as might be, often with an unforgettable memory.
Does checkers offer the same level of excitement? Certainly! Today we bring you a problem that will make you sit up in your seat.

WHITE
White to Play and Win
W:W31,30,22,17,16,14,10:B24,K21,18,15,8,7,3.
This is a stroke problem that is supposed to an "easy" one, but we have our doubts about that unless your powers of visualization are very well developed. We'd call it at least "medium" in difficulty, but as a pleaser, it surely rates way up there.
Stroke problems may not be practical, but they are great fun, and they develop our ability to look ahead. Give this one a try and see if you aren't just a little taken in by the spectacular conclusion. As always, clicking on Read More will show you the winning moves.![]()
Medium Problem

No, we don't mean that kind of "medium" and we don't expect you to divine the solution to today's checker problem; rather, we consider it "medium" in difficulty. It's a nice setting sent to us by Toronto's intrepid checkerists, Lloyd and Josh Gordon.

BLACK
Black to Play and Draw
B:W32,30,22,K19:B27,23,21,3.
The stars tell us you'll be able to solve this one, as long as you keep your thinking channels open. It won't take a seance, though, to check your solution; all you need do is wave your mouse on Read More to see how it's done.![]()
The Checker Maven is produced at editorial offices in Honolulu, Hawai`i, as a completely non-commercial public service from which no profit is obtained or sought. Original material is Copyright © 2004-2025 Avi Gobbler Publishing. Other material is public domain, as attributed, or licensed under Creative Commons. Information presented on this site is offered as-is, at no cost, and bears no express or implied warranty as to accuracy or usability. You agree that you use such information entirely at your own risk. No liabilities of any kind under any legal theory whatsoever are accepted. The Checker Maven is dedicated to the memory of Mr. Bob Newell, Sr.

