The Checker Maven
Jump to navigationMachine Learning Comes To Kingsrow

Computers have progressed a very, very long way since their earliest days. It may not be quite as well known, though, that computers have been programmed to play games since almost the very beginning. But we doubt that the hardy coding pioneers of the time would have dreamed just how far the state of the art has come since then.
Certainly well known today are Google's phenomenal Alpha game playing programs, which contain self-teaching or "machine learning" methods. After years and years of computer Go programs barely reaching respectable playing levels, AlphaGo appeared on the scene and defeated one of the world's highest ranked Go players, something no one ever expected. And AlphaChess very quickly became able to defeat even the strongest chess playing programs around. Machine learning is here to stay, and the results are phenomenal.
Of course, it's not new. The idea was proposed by an IBM scientist over 60 years ago. But implementing it successfully was the issue, for to succeed, the computer programs would have to "train" on millions and millions of different game positions. That wasn't a realistic possibility until relatively recent years.
The method worked well at first for non-deterministic games--- games with an element of luck. Gnu Backgammon played at the master level, as did others. But applications to checkers largely failed. Blondie 24 was a lot of fun but never a serious competitor, and NeuroDraughts wasn't fully developed.

Ed Gilbert
Photo Credit: Carol Gilbert
All that has changed, though, with renowned checker engine programmer Ed Gilbert's latest developments for his world class Kingsrow computer engine. Ed was kind enough to send us the details. The following was written by Ed Gilbert with input from Rein Halbersma.
The latest Kingsrow for 8x8 checkers is a big departure from previous versions.
Until recently, Kingsrow used a manually built and tuned evaluation function. This function computes a numeric score for a game position based on a number of material and positional features. It looks at the number of men and kings of each color, and position attributes including back rank formation, center control, tempo, left-right balance, runaways (men that have an open path to crowning), locks, bridges, tailhooks, king mobility, dog-holes, and several others. Creating this function requires some knowledge of checkers strategy, and is very time consuming.
The latest Kingsrow has done away with these manually constructed and tuned evaluation features. Instead it is built using machine learning (ML) techniques which require no game specific knowledge other than the basic rules of the game. It has learned to play at a level significantly stronger than previous versions entirely through self-play games.
In a test match of 16,000 blitz games (11-man ballot, 0.3 seconds per move), it scored a +72 ELO advantage over the best manually built and tuned eval version. There were more than 5 times as many wins for the ML Kingsrow as losses.
The ML eval uses a set of overlapping rectangular board regions. These regions are either 8 or 12 squares, depending on whether kings are present. For every configuration of pieces on these squares, a score is assigned by the machine learning process. A position evaluation is then simply the sum of the scores of each region, plus something for any material differences in men and kings. In the 8-square regions, each square can either be empty or occupied by one of the four piece types, so there are total of 5^8 = 390,625 configurations. In the 12-square regions there are no kings, so there are 3^12 = 531,441 configurations.
To compute values for each configuration, a large number of training positions are needed. I created a database of approximately one million games through rapid self-play. Each game took about 5 seconds. The positions are extracted from the games, and each position is assigned the win, draw, or loss value of the game result. Initially the values in the rectangular board regions are assigned random values. Through a process called logistic regression, the values are adjusted to minimize the mean squared error when comparing the eval output of each training position to the win, draw, or loss value that was assigned from the game results.
Similar machine learning techniques have been used in other board game programs. In 1997, Michael Buro described a similar process that he used to build the evaluation function for his Othello program named Logistello. In 2015, Fabien Letouzey created a strong 10x10 international draughts program named Scan using an ML eval, and around this time Michel Grimminck was using a ML eval in his program Dragon. Since then other 10x10 programs have switched to ML evals, including Kingsrow, and Maximus by Jan-Jaap van Horssen. I think that the English and Italian variants of Kingsrow are the first 8x8 programs to use an ML eval.
Ed's new super-strong version of KingsRow is available for free download from his website. Combine that with his 10-piece endgame database, and you'll have by far the strongest checker engine in the world, a fearsome competitor and an incredible training partner.
Let's look at a few difficult positions, some of which were analyzed by human players for years and even by reasonably strong computer engines for hours. KingsRow ML solved each and every one of them virtually instantly.
First, the so-called "100 years problem" (as in Boland's Masterpiece, p. 125 diagram 1).
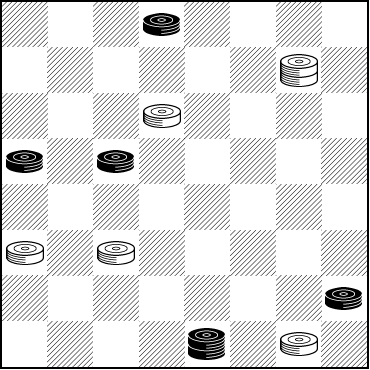
WHITE
White to Play, What Result?
W:WK8,10,21,22,32:B2,13,14,28,K31.
Next, the Phantom Fox Den, from Basic Checkers 2010, p. 260.

WHITE
White to Play, What Result?
W:W16,21,22,23,27,31,32:B1,3,7,10,11,14,20.
And finally, a position suggested by Richard Pask, from Complete Checkers p. 273 halfway down, where Mr. Pask notes: "12-16?! has shock value ..."

WHITE
White to Play, What Result?
W:W17,19,21,22,25,26,27,28,29,31:B2,3,4,9,10,11,13,14,16,20.
Surely we don't expect you to solve each of these (unless you wish to), but do look them over and at least form an opinion. Then click on Read More and be amazed.![]()
Solutions
Here are the main lines of play given by Kingsrow ML. For Phantom Fox Den and Pask Position the runups are included with the solution.
100 Years Problem:
8-11 14-17 21x14 31-26 22-18 26-22 11-15 22-17 15-19 etc. Drawn.
Phantom Fox Den:
10-15 23-18 12-16 26-23 16-19 23x16 11x20 18x11 8x15 22-18 15x22 25x18 4-8 24-19 8-11 29-25 9-14 18x9 5x14 25-22 6-10 30-26 11-15 26-23 15x24 28x19 7-11 19-16 2-7 31-26 11-15 32-28 1-5 22-17 20-24 27x20 15-18 23-19 18-22 26-23 22-26 16-11 7x16 19x12 26-31 23-19 31-26 17-13 14-18 19-16 10-15 16-11 18-22 21-17 26-23 11-8 22-25 17-14 25-30 8-4 30-26 4-8 15-19 14-10 and the White Win is assured.
Pask Position:
10-14 24-19 7-10 28-24 11-16 32-28 16-20 22-17 9-13 25-22 5-9 19-15 10x19 24x15 6-10 15x6 1x10 23-19 8-11 30-25 12-16 19x12 11-16 27-23 2-6 22-18 13x22 26x17 16-19 23x16 14x23 16-11 10-15 28-24 20x27 31x24 23-26 17-13 26-31 25-22 31-27 24-20 15-19 20-16 19-24 11-7 3x10 16-11 9-14 22-17 27-23 12-8 14-18 8-3 10-15 11-7 15-19 7-2 6-10 3-7 10-15 7-11 23-27 17-14 19-23 14-10 23-26 10-7 26-31 2-6 31-26 13-9 15-19 7-3 26-22 and the game now evaluates to a highly probable draw.
Great stuff. Our thanks to Ed Gilbert for providing us with material for this column.
You can email the Webmaster with comments on this article.
